6. CMOS

Having explored the powerful combinational device abstraction as a model for our logical building blocks, we turn to the search for a practical technology for production of realistic implementations that closely match our model. Our technology wish list includes:

• High gain and nonlinearity, as discussed in Section 5.6, to maximize noise immunity.
• Low power consumption. Some power will be used as changing signal levels cause current to flow in out out of parasitic capacitances, but an ideal technology will consume no power when signals are static.
• High speed. Of course, we'd like our devices to maximize performance (implying that $t_{pd}$ propagation delays be minimized and physical sizes be small.
• Low cost.

During the few decades that electronic digital systems have exploded on the engineering scene, a number of nonlinear device technologies have been used -- ranging from electromagnetic relays to vacuum tubes and diodes. The advent of semiconductor electronics and the miniaturization push of integrated circuits, technology breakthroughs roughly contemporaneous with the digital revolution, opened the way to incorporation of billions of active devices (transistors) on the surface of a small silicon chip. A remarkable succession of engineering improvements have allowed the number of transistors on a chip to double roughly every two years for the last 5 decades, a phenomenon popularly referred to as Moore's Law after its observation in 1965 by Intel founder Gordon Moore.

One technology, CMOS (for Complementary Metal-Oxide Semiconductor), has emerged as the logic technology of choice, getting high marks in each dimension of our wish list. We, like most of industry, will focus on CMOS as our choice for implementing logic devices.

6.1. MOSFETs

The nonlinear circuit element in CMOS is the MOSFET or Metal Oxide Semiconductor Field Effect Transistor, whose physical structure is sketched below. MOSFETs are used in CMOS logic as voltage-controlled switches: current may or may not flow between two MOSFET terminals called the source and the drain depending on the voltage on a third terminal, the gate, which separates them.

An important feature of MOSFETs is that no steady-state current flows between the gate terminal and the source and drain: the gate behaves as if it is coupled to the other terminals through a capacitor. Current flows into and out of the gate terminal only when the gate voltage changes, and then only until the charge on the gate reaches an equilibrium that matches the voltage drop. This allows MOSFETs to draw no gate current while quiescent (i.e., when logic values are constant); if we design our CMOS circuits so that source and drain currents of quiescent circuits are zero as well, we can achieve the goal of zero quiescent power dissipation. We will adopt shortly a cookbook formula that offers this major power advantage.

6.1.1. NFETs and PFETs

A key to CMOS circuit design is manufacturing technology that allows fabrication of two different types of MOSFET on a single silicon surface. The two flavors of transistor are the N-channel and P-channel FET, which perform complementary functions in CMOS devices (hence the C in CMOS). Each FET is a four-terminal device; however our stylized use of NFETs and PFETs involves connecting the $B$ (Bulk) terminal to ground or $V_{DD}$ respecively, and using them as three-terminal circuit components.

The figure to the right shows the circuit symbol for an NFET, along with a sketch of its physical layout and circuit models for its behavior as a voltage-controled switch. The transistor is fabricated by embedding n-type (doped) source and drain terminals in a p-type substrate, which is connected to ground via the $B$ (Bulk) terminal. The gate electrode controls the flow of current between source and drain: if the voltage $V_{GS}$ between the gate and the source is less than a threshold $V_{TH,NFET}$, no current flows between source and drain: the transistor behaves like an open switch. If $V_{GS}$ is above the $V_{TH,NFET}$ threshold, current flows from drain to source, impeded by a small "on" resistance. A typical switching threshold voltage is about a half volt. If we connect the source of an NFET to ground, it provides an effective means of selectively grounding the node connected to its drain by changing its gate voltage.

The complementary PFET is made by embedding a well of n-type silicon in the p-type substrate, and connecting the n-type well to the power supply voltage $V_{DD}$ via terminal $B$ in the figure. Within that well, the PFET transistor is fabricated using opposite-polarity dopings from those of the NFET: the source and drain are made of p-type silicon. The circuit symbol for the PFET is similar to that of the NFET, with the addition of an small circle at the gate terminal: these so-called inversion bubbles are widely used in logic symbols to indicate that the sense of a signal is opposite of what it would be without the bubble. In the case of the PFET, it flags the fact that the switch behavior is opposite of the NFET's: $V_{GS}$ above a threshold value makes the PFET source/drain connection look like an open switch, while $V_{GS}$ below the threshold connects source to drain through a low "on" resistance. A PFET whose source is connected to the power supply voltage $V_{DD}$ provides an effective way to selectively connect its drain to $V_{DD}$.

6.1.2. Transistor Sizing

Design parameters for each transistor include its physical dimensions, which effect its current- and power-handling capacity. It is common to parameterize FETs by the width and length of the channel between the source and drain, in scaled distance units: length is the distance between source and drain, while width is the width is the length of the channel/source and channel/drain boundaries. Of particular interest is the ratio between the width and length of the channel, which determines the "on" resistance and hence the current carrying capacity of the source-drain connection when the transistor is "on". In general, the drain-source current $I_{DS}$ is proportional to the $Width/Length$ ratio.

While we will largely ignore transistor sizing issues in our subsequent circuits, this parameter can play an important role in the optimization of performance and energy consumption of a digital circuit. A device whose output drives a long wire or heavy capacitive load, for example, may benefit from tuning of transistor sizes to provide higher-current output.

6.2. Pullup and Pulldown Circuits

Each of the NFET and PFET devices behaves as a voltage-controlled switch, enabling or disabling a connection between its source and drain terminals depending on whether its gate voltage is above or below a fixed threshold. Our intention is to select logic mapping parameters as described in Section 5.4.1 that place the FET switching thresholds reliably in the forbidden zone, so that valid logic levels applied to gate terminals of NFETs and PFETs will open or close their source/drain connections. By using logic levels to open and close networks of switches, we can selectively drive output terminals of logic devices to ground ($0$ volts) or $V_{DD}$ (power supply voltage), which represent maximally valid 0s and 1s respectively.

In general, each logical output of a device will selectively connect to ground through a pulldown circuit and will selectively connect to $V_{DD}$ through a pullup circuit, where the pulldown and pullup circuits contain FETs whose gates are connected to logical inputs. Given our goals of (a) driving each output to a valid logic level for each input combination and (b) zero quiescent current flow, it is important that exactly one of the pullup/pulldown circuits present a closed circuit for any input combination. If neither circuit conducts, the output voltage will "float" at some unspecified value, likely invalid; if both conduct, a low-resistance path between $V_{DD}$ and ground will dissipate excessive power and likely do permanent damage to the circuit.

NFETs are well suited for use in pulldown circuits since they can connect the output terminal to ground potential via a small "on" resistance but without a threshold voltage drop between the output voltage and ground; for similar reasons, PFETs are a nearly ideal choice for use in pullup circuits. Consequently CMOS combinational logic devices (commonly called "gates", not to be confused with the gate terminal of a MOSFET) use only PFETs in pullup circuits and NFETs in pulldowns. The main cleverness required in the design of a CMOS gate is to come up with pullup and pulldown circuits that are properly complementary -- that is, to design the circuits so that for every combination of logical inputs, either the pullup or the pulldown is active but not both.

Recalling that an NFET is active (conducts) when its gate voltage is high (a logic 1) and PFET is active when its gate voltage is low (a logical zero), we can construct the simplest "interesting" CMOS gate: an inverter. The inverter uses a single PFET pullup and a single NFET pulldown as shown to the left. Its logical input is connected to the gate terminals of both the PFET pullup and the NFET pulldown, turning on the pulldown path when its value is 1 and turning on the pullup path when its value is 0, causing the output voltage to represent the opposite logic level from its input. We arrange that $V_{il}$ is well below the switching threshold of both transistors, so that a valid 0 input causes the pullup to conduct and the pulldown to present an open circuit; similarly, ensuring $V_{ih}$ is well above the thresholds assures the output terminal to be connected to ground and not $V_{DD}$ on a valid 1 input.

If we plot the voltage transfer curve of the CMOS inverter, we get something like that shown to the right: the high gain near the switching thresholds of the transistors is confined to the forbidden zone of our logic mapping, neatly avoiding the shaded regions corresponding to invalid outputs caused by valid inputs. The pullup/pulldown architecture of CMOS gates assures that $V_{OH}$ and $V_{OL}$ can be close to $V_{DD}$ and 0, respectively, while $V_{IL}$ and $V_{IH}$ need only bracket the nearly vertical steps at the transistor switching thresholds. This combination leads to good noise margins.

Recall that the voltage transfer curve represents an equilibrium output voltage for each input voltage.

It can be made using a test setup similar to that shown on the left, where successive input voltages are applied to our inverter input, and enough time is allowed to elapse to let $V_{out}$ stabilize. Even with nothing connected to the output terminal, this may take some time due to parasitic capacitances, resistances, and inductances. At equilibrium, $V_{out}$ will be constant and $i_{pu} = i_{pd}$: there will be no output current, so any current flowing through the pullup must continue through the pulldown. Once this equilibrium is reached, $V_{out}$ is recorded on our voltage transfer curve and we move on to the next input voltage.

6.2.1. Series and Parallel Connections

Pullup and pulldown circuits for logic functions of multiple inputs involves configuring series and parallel connections of PFETs (in pullups) or NFETs (in pulldowns), again with each gate terminal connected to one logical input.

A quick review of parallel and series connection of "switching" circuits:

	Assume that the notation shown to the left represents a circuit that conducts when some circumstance we call $A$ is true, and otherwise presents an open circuit between its two terminals.
	Then the series circuit shown to the left conducts only when both $A$ and $B$ are true: if either $A$ or $B$ is false, the corresponding circuit will open and no current will flow. This allows us to effect a logical AND between the conditions $A$ and $B$.
	Similarly the parallel circuit shown to the left represents a circuit that conducts when either $A$ or $B$, or both $A$ and $B$, are true. This effects a logical OR between the conditions $A$ and $B$.

Using series and parallel combinations of circuits containing NFETs and PFETs, we can build pullup and pulldown circuits that are active -- pull an output to ground or $V_{DD}$ -- based on ANDs and ORs of logic values carried on input wires.

6.2.2. Complementary circuits

The remaining ingredient to our CMOS formula is the requirement that we connect each output to complementary pullups and pulldowns -- that is, that the pullup on an output is active on exactly the combination of input values for which the pulldown on that output is not active.

Circuit	Complement	Description
		Notation: The bar over the condition A indicates a circuit that is active when $A$ is not true; thus the two circuits to the left are complementary.
		Given a series connection of circuits active on $A$ and $B$, we can construct its complement by the parallel connection of complementary circuits $\bar A$ and $\bar B$.
		Given a parallel connection of circuits active on $A$ and $B$, we can construct its complement by the series connection of complementary circuits $\bar A$ and $\bar B$.
		Finally, we observe that an NFET connected to an input $A$ is the complement of a PFET connected to the same input: the NFET presents a closed circuit when $A$ is a logical 1, while the PFET closes when $A=0$ as we observed in the CMOS inverter.

The astute reader will notice that the above observations gives us a powerful toolkit for building complementary pullup and pulldown circuits based on combinations of input values. The NFET/PFET rule allows us to build pullups/pulldowns for single variables, as we did in the inverter; the series/parallel constructions allow us to combine pullups or pulldowns for several variables, say $A$ and $B$, to make pullups or pulldowns for logical combinations such as the AND or OR of $A$ and $B$.

Because of the electrical characteristics of PFETs and NFETs, CMOS gates use only PFETs in pullup circuits and NFETs in pulldown circuits. Thus each output of a CMOS gate is connected to a pullup circuit containing series/parallel connected PFETs, as well as a complementary pulldown circuit containing parallel/series connected NFETs.

It is worth observing that

1. For every PFET-based pullup circuit, there is a complementary NFET-based pulldown circuit and vice versa.
2. Given a pullup or pulldown circuit, one can mechanically construct the complementary pulldown/pullup circuit by systematically replacing series with parallel connections, parallel with series connections, PFETs with NFETs, and NFETs with PFETs. The resulting ciruits are duals of one another, and are active under complementary input combinations.
3. Our restrictions to PFETs in pullups and NFETs in pulldowns makes single CMOS gates naturally inverting: a logical 1 on an input can only turn on an NFET and turn off a PFET. This limits the set of functions we can implement as single CMOS gates: certain functions require multiple CMOS gates in their implementation.

6.3. The CMOS Gate Recipe

We use the term CMOS gate to refer to a single-output combinational device implemented as shown to the right. The output node is connected to $V_{DD}$ via a pullup consisting of zero or more PFETs, and is connected to ground via a pulldown consisting of zero or more NFETs. The device has zero or more logical inputs, and the gate terminal of each PFET or NFET is connected to one such input.

In the typical CMOS gate,

• The pullup and pulldown circuits are duals of each other, in the sense described in Section 6.2.2.
• Each input connects to one or more PFETs in the pullup, and to an equal number of NFETs in the dual pulldown circuit. An exception is the degenerate case of a CMOS gate whose output is independent of one or more inputs; in this case, the ignored inputs are not connected to anything.
• For the above reasons, a single CMOS gate typically comprises an even number of transistors, with equal numbers of NFETs and PFETs.

Our specification of "zero or more" transistors in the pullup/pulldown circuits allows us to include the degenerate extremes as CMOS gates: devices which ignore all their inputs and produce a constant 0 or 1 as output by connecting the output node to $V_{DD}$ or ground.

In general, we can approach the design of a CMOS gate for some simple function F by either

• Designing a pulldown circuit that is active for those input combinations for which $F=0$, or
• Designing a pullup circuit that is active for those input combinations for which $F=1$

and then systematically deriving the complementary pullup/pulldown circuit by taking the dual of the circuit we've designed. Finally, we combine them to make the CMOS gate per the above diagram.

6.3.1. Common 2-input gates

A simple application of the above recipe can be used to implement the popular 2-input NAND gate, whose circuit symbol and truth table are shown to the right. The name NAND derives from "Not AND", reflecting the fact that the gate's output is the inverse of the logical AND of its two inputs. The circuit symbol, similarly, consists of a shape conventionally used to depict an AND operation -- having a straight input side and a curved output side -- with a small circle (or bubble) at its output which conventionally denotes inversion.

From the NAND truth table, we observe that the gate output should be zero if and only if both input values are 1, dictating a pulldown that is active (conducting) when the A and B inputs both carry a high voltage.

The pulldown is handily constructed from a series-connected pair of NFETs between the output node and ground, as shown in the diagram to the left. The complementary pullup circuit is the dual of the pulldown, consisting of parallel-connected PFETs between the output C and the supply voltage $V_{DD}$, again as shown in the diagram. The gate element of each FET in the pullup and pulldown circuits is connected to one of the logical inputs ($A$ or $B$) to our CMOS gate, causing logical input combinations to open and close the FET switches effecting an appropriate connection of the output $C$ to $V_{DD}$ or ground according to the values in the truth table.

Alternatively, the use of parallel-connected NFETs in the pulldown and series-connected PFETs in the pullup yields a CMOS implementation of the NOR gate whose circuit symobl and truth table are shown to the right. Again, the symbol is a composite of the standard symbol for a logical OR with an inversion bubble on its output, indicating a "Not OR" or NOR operation. The corresponding CMOS implementation is shown to the left.

The CMOS implementation of a 2-input NAND gate can be easily extended to NAND of 3-, 4- or more inputs by simply extending the series pulldown chain and parallel pullup with additional FETs whose gate elements connect to the additional logical inputs. Similarly, the 2-input NOR gate can be extended to 3 or more input NOR operations by adding an NFET/PFET pair for each additional logical input. Electrical considerations (such as delays due to parasitics) usually limit the number of inputs of single CMOS gates (the so-called fan-in) to a something like 4 or 5; beyond this size, a circuit consisting of several CMOS gates is likely to offer better cost/performance characteristics.

6.4. Properties of CMOS gates

The CMOS gate recipe of an output node connected complementary PFET-based pullup and NFET-based pulldown circuits offers a nearly ideal realization of the combinational device abstraction, since

• For each input combination, it will drive its output to an equilibrium voltage of 0 (ground) or $V_{DD}$, generating ideal representations of logical $0$ or $1$.
• At equilibruim, the FETs used in the pullup/pulldown circuits draw zero gate current. This implies that CMOS gates draw zero input current once parasitic capacitances have been charged to equilibrium, hence CMOS circuits have zero static power dissipation.

In the following sections, we will explore additional consequences of the CMOS gate design regimen.

6.4.1. CMOS gates are inverting

It may seem peculiar that the example CMOS gates chosen for Section 6.3.1 include NAND and NOR but not the conceptually simpler logical operations AND and OR. In fact, this choice reflects a fundamental constraint of CMOS: only certain logical functions -- inverting functions -- can be implemented as a single CMOS gate. Other functions may be implemented using CMOS, but they require interconnections of multiple CMOS gates.

To understand this restriction, consider the effect of an input to a CMOS gate on the voltage on its output node. A logical $0$ -- a ground potential -- can only affect the output by turning off NFETs in the pulldown and turning on PFETs in the pullup, forcing the output to a logical $1$. Conversely, an input $1$ can only effect the output voltage by driving it to a logical $0$. This constraint is consistent, for example, with a k-input NOR operation, where a $1$ on any input forces the output to become $0$; however, it cannot represent a logical $OR$, where a $1$ on any input must force the output to become a $1$. Thus we can implement k-input NOR as a single CMOS gate, but to implement k-input OR we use a k-input NOR followed by an inverter.

We can determine whether a particular function F can be implemented as a single CMOS gate by examining pairs of rows of its truth table that differ in only one input value. Changing an input from $0$ to $1$ can only effect a $1$-to-$0$ change on the output of a CMOS gate, or may leave the output unchanged; it cannot cause a $0$-to-$1$ output change. Nor can a $1$-to-$0$ input change cause a $1$-to-$0$ output change. Thus the observation that $F(0,1,1)=1$ but $F(0,0,1)=0$ causes us to conclude that the function $F$ cannot be implmented as a single CMOS gate.

To generalize slightly, suppose that we know that some 3-input function $F$ is implemented as a single CMOS gate, and that $F(0,1,1)=1$. Since changing either of the input $1$s to $0$ can only force the output to become $1$, that implies $F(0,x,y)=1$ for every choice of $x$ and $y$, an observation that we might denote as $F(0,*,*)=1$ using $*$ to denote an unspecified "don't care" value. Similarly, knowing that $F(1,0,1)=0$ implies that $F(1,*,1)=0$ since changing the second argument from $0$ to $1$ can only force the already-$0$ output to $0$.

Knowing that the output of a CMOS gate is $0$ for some particular set of input values assures us that the $1$s among its inputs are turning on a set of NFETs in its pulldown that connects its output node to ground: its output will be zero so long as these input $1$s persist, independently of the values on the other inputs. Similarly, knowing that a CMOS gate output is $1$ for some input combination assures us that the $0$s among the inputs enable a pullup path between the output and $V_{DD}$, independently of the other inputs.

Taking these observations to the extreme, a CMOS gate whose output is $1$ when all inputs are $1$ can only be the degenerate gate whose output is always $1$ independently of its inputs, and similarly for the gate whose output is $0$ given only $0$ input values.

6.4.2. CMOS gates are lenient

We can take the observations of the previous section one step further to show that CMOS gates are lenient combinational devices as described in Section 5.9.2. Recall that lenience implies the additional guarantee of output validity when a subset of the inputs have been stable and valid for $t_{PD}$, so long as that input subset is sufficient to determine the output value. For example, if the truth table of a 3-input lenient gate $G$ specifies that $G(0, 0, 1) = 1 = G(0, 1, 1)$, which we abbreviate as $G(0, *, 1) = 1$, then $G$'s lenience assures that its output will be $1$ whenever its first input has been $0$ and its third input has been $1$ for at least $t_{PD}$, independently of the voltage (or validity) of its second input.

If $G$ is implemented as a single CMOS gate, this lenience property follows automatically. In our example, the $G(0, *, 1) = 1$ property of the truth table dictates a pullup with a path that connects the output to $V_{DD}$ whenever the first input is $0$, viz. a PFET gated by the first input between the output node and $V_{DD}$. This connection is independent of the second input as dictated by the truth table, and is in fact independent of the third input since PFET paths can only be turned on by $0$ inputs. Because of the complementary nature of the pulldown circuitry, a $0$ value on $G$'s first input must turn off an NFET in every path between the output node and ground, disabling the pulldown. Thus a $0$ on the first input electrically connects the output node to $V_{DD}$ independently of the voltages on the other two inputs: they may represent valid $0$, valid $1$, or be invalid (in the forbidden zone).

An analogous argument can be made for a CMOS gate $G$ whose value is $0$ (rather than $1$) for some subset of input values, e.g. if $G(0, *, 1) = 0$. In this case, $G$'s output must be connected to ground via some NFET in the pulldown gated by the third input, and that connection is assured by the $G(*, *, 1)$ input pattern independently of the voltages on the first two inputs.

As a concrete example, consider the functional specification of a 2-input NOR gate shown to the right. Consider an experiment where we hold one input -- $A$ -- of the NOR gate at a logical $1$, and make a transition on the other input from $1$ to $0$ as shown in the diagram to the left. Consulting the NOR truth table, both the initial output of the gate (prior to the input transition) and its final output should be $0$. Assuming only that the gate obeys the specifications as a combinational device, the output $C$ is constrained to be $0$ until $t_{CD}$ following the input transition, and again $t_{PD}$ after the transition; however, it is completely unspecified between the ends of the $t_{CD}$ and $t_{PD}$ windows. During this time it may exhibit a "glitch", even becoming a valid $1$ multiple times, before settling to its final value of $0$.

This behavior is completely consistent with the combinational device abstraction, and is usually unobjectionable in practice. But consider repeating the above experiment using our CMOS implementation of NOR, shown to the right. The connection of the $A$ input to a constant $1$ has the effect of turning off one of the series-connected PFETs in the pullup, isolating the output from $V_{DD}$; it also turns on one of the parallel-connected NFETs in the pulldown, assuring a connection between the output and ground. The $A=1$ constraint thus assures an output of $0$ independently of the input $B$, which can be either logic value (or invalid) without compromising the output so long as $A$ remains $1$. In addition to obeying the rules for a combinational device, the CMOS implementation is lenient: its output validity is assured by any subset of inputs sufficient to determine an output value, and is uneffected by changes on other inputs.

Generalizing, if we consider various paths through the pullup and pulldown circuits of a CMOS gate we can systematically constuct rows of a lenient truth table (containing don't-care inputs, written as $*$). Each path between the output and ground through the pulldown circuit determines a set of inputs (those gating the NFETs along the path) capable of forcing the output to $0$; similarly, each path through the pullup circuit determines a set of inputs capable of forcing a $1$ output. Whenever the inputs along a pullup path are all $0$ the gate output will be $1$, and whenever the inputs along a pulldown path are all $1$ the gate will output a $0$. Each of the pullup paths corresponds to a truth table line whose inputs are $0$s and $*$s and whose output is $1$; each of the pulldown paths corresponds to a line with $1$ and $*$s as inputs and a $0$ output. In general, the behaviour of every single CMOS gate can be described by a set of such rules, and conforms to our definition of a lenient combinational device.

It is important to note that, while every single CMOS gate is lenient, combinational devices constructed as circuits whose components are CMOS gates are not necessarily lenient. This topic will be revisited in Section 7.7.1.

6.4.3. CMOS gate timing

As combinational devices, the timing of a CMOS gate is characterized by two parameters: its propagation delay $t_{PD}$, an upper bound on the time taken to produce valid outputs given valid inputs, and its contamination delay $t_{CD}$, a lower bound on the time elapsed between an input becoming invalid and the consequent output invalidity. The physical basis for these delays is the time required to change voltage on circuit nodes due to capacitance, including the unavoidable parasitic capacitance discussed in Section 4.3.1.

Consider a CMOS inverter whose output connects to another inverter, as shown to the right. The output node is characterized by some capacitive load, $C$, which includes both intrinsic capacitance of connected inputs as well as parasitic capacitance of the wiring. When the input $V_{IN}$ to the left inverter makes a transition from $1$ to $0$, it enables current to flow through the pullup to the output node and charge this capacitance, at a rate proportional to the current flow through the enabled pullup. This current is limited by the non-zero on resistance of the enabled PFET, as well as parasitic resistance of the wiring itself. The result is an exponential rise of the output voltage toward $V_{DD}$ whose time constant is the product of the capacitance $C$ and the resistance, much like the example of Section 4.3.1. When a device output changes from a logical $0$ to a logical $1$, we will observe an exponential rise or fall toward the target value; we often refer to the time taken for this curve to go from a valid $0$ to a valid $1$ as the rise time of the signal, and to the timing of its opposite transition as the fall time. There will typically be a brief delay prior to the rise or fall time corresponding to the propagation of a changed input value through the affected pullup and pulldown transistors as shown to the right.

6.4.4. Delay specifications

The combinational device abstraction of Chapter 5, based as it is on the idealized circuit theoretic model of components connected by equipotential nodes, requires that we bundle the timing behavior discussed in the prior section into the $t_{PD}$ and $t_{CD}$ timing specifications of devices driving each digital output node.

The contamination delay $t_{CD}$ specifies a lower bound on the time a previously-valid output will remain valid after an input change; we choose this parameter to conservatively reflect the minimum interval required for an input change to propagate to affected transistors and begin their turnon/turnoff transition. Often we specify contamination delay as zero, which is always a safe bound; in certain critical situations, we choose a conservative non-zero value to guarantee a small delay between input and output invalidity.

Since the propagation delay $t_{PD}$ specifies an upper bound on the time between an input stimulus and a valid output level, it should be chosen to conservatively reflect the maximum delay (including transistor switching times and output rise/fall times) we anticipate. We might make this selection after testing many samples under a variety of output loading and temperature circumstances, extrapolating our worst-case observations to come up with a conservative $t_{PD}$ specification.

The $t_{PD}$/$t_{CD}$ timing model gives our digital abstraction simple and powerful analysis tools, including the ability to define provably reliable combinational circuits (the subject of Section 5.3.2) as well as sequential logic (Chapter 8). However, it squarely confronts the major dilemma previewed in Section 4.5.2: the abstraction of space from the circuit-theoretic model of signal timing. In practice, the timing of the output of a CMOS gate depends not only on intrinsic properties of the gate itself, but also on the electrical load placed on its output by connected devices and wiring. The delay between an input change to an inverter and its consequent valid output cannot realistically be bounded by an inverter-specific constant: it depends on the length and routing of connected wires and other device inputs. The fact that wire lengths and routing are determined late in the implementation process distinguishes these factors as implementation details rather than properties of a specified digital circuit, a fact that simply violates the constraints of our digital circuit abstraction.

Fortunately, the properties of CMOS as an implementation technology offer opportunities to reach a workable compromise between the simplicity and power of our propagation-delay timing model and realistic physics of digital systems. In particular, the fact that CMOS devices draw no steady-state input current implies that the output of a CMOS gate will eventually reach its valid output value; its simply not practical to bound the time this will take without consideration of wiring and loading details. Thus we can design circuits using "nominal" values for $t_{PD}$ specifications -- chosen using light loading -- and design circuits that will operate properly but whose overall timing specifications may turn out to be optimistic once wiring is taken into account. In Section 8.3.3, we describe an engineering discipline for designing systems with a single timing parameter -- a clock period -- that controls the tradeoff between computational performance and the amount of time allowed for signals on every circuit node to settle to their target values. Systems we design using this discipline will be guaranteed to work for some (sufficiently slow) setting of this parameter, as sketched in Section 4.5.2.1.

We will revisit this issue in later chapters. For now, we will assign nominal propagation delays to devices, and design and analyze our circuits using the fictitious promise made on their behalf by the combinational device abstraction.

6.5. Power Consumption

An attractive feature of CMOS technology for digital systems is the fact that, once it reaches a static equilibrium and all circuit nodes have settled to valid logic levels, no current flows and consequently no power is dissipated. This property implies that the power consumption of a CMOS circuit is proportional to the rate at which signals change logic levels, hence -- ideally -- to the rate at which useful computation is performed.

The primary cause of current flow within a CMOS circuit is the need to charge and discharge parasitic capacitances distributed among the nodes of that circuit, and the primary mechanism for energy consumption is the dissipation of energy (in the form of heat) due to ohmic losses as these currents flow through the incidental resistances in wires and transistors.

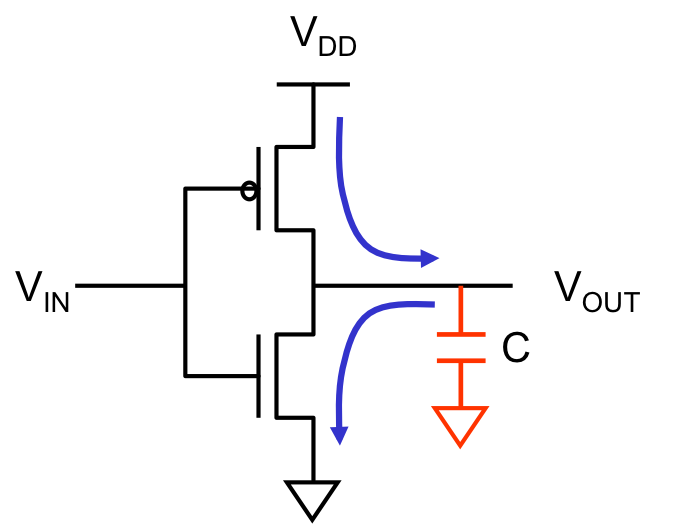
Consider, for example, the operation of the CMOS inverter shown to the right as its input voltage switches from a valid $0$ to a valid $1$ and back again to a valid $0$. The output node is inevitably coupled to ground (as well as $V_{DD}$ and perhaps other signal wires) by some parasitic capacitance, shown in the diagram as a lumped capacitor to ground. If the initial $V_{IN}$ is zero (corresponding to a valid logical $0$), the equilibrium $V_{OUT}$ is $V_{DD}$; at this static equilibrium, no current flows, but the charged capacitor has a stored energy of $C\cdot V_{DD}^2/2$ joules, where $C$ is the total capacitance. If $V_{IN}$ now makes a transition to $V_{DD}$ (a valid $1$), the pullup PFET opens and the pulldown closes, providing a low-resistance path between the output node and ground; the capacitance discharges through this path, until it reaches its new equilibrium $V_{OUT}=0$. The capacitor now has been discharged to zero volts: it has lost the $C\cdot V_{DD}^2/2$ joules of energy it previously stored. This energy has in fact been converted to heat by the flow of current through the resistance along its discharge path.

A subsequent $1 \rightarrow 0$ transition on $V_{IN}$ will open the pulldown and close the pullup, charging the output capacitance back to $V_{DD}$ and dissipating another $C\cdot V_{DD}^2/2$ joules by ohmic losses from the necessary current flow. The total energy dissipation from this $0 \rightarrow 1 \rightarrow 0$ cycle is $C \cdot V_{DD} ^2$ joules.

Similar energy losses occur at each node of a complex CMOS circuit, at rates proportional to the frequency at which their logic values change. If we consider a system comprising $N$ CMOS gates cycling at a frequency of $f$ cycles/second, the resulting power consumption is on the order of $f \cdot N \cdot C \cdot V_{DD} ^ 2$ watts. As a representative example, a CMOS chip comprising $10^8$ gates driving an average output capacitance of $10^{-15}$ farads using $V_{DD} = 1$ volt and operating at a gigahertz ($10^9$) frequency would consume about $10^8 \cdot 10^9 \cdot 10^{-15} \cdot 1^2 = 100$ watts of power, all converted to heat that must be conducted away from the chip.

The constraint of power (and consequent cooling) costs has been a prime motivator for technology improvements. Historic trends have driven the number of gates/chip higher (due to Moore's law growth in transistors per chip), and -- until recently -- operating frequencies have increased with each generation of technology. These trends have been partially offset by scaling of CMOS devices to smaller size, with proportionate decreases in capacitance. Lowering operating voltage has been a particular priority (due to the quadratic dependence of power on voltage), but the current 1 volt range may be close to the lower limit for reasons related to device physics.

6.5.1. Must computation consume power?

The costs of energy consumption (and related cost of cooling) have emerged as a primary constraint on the assimilation of digital technologies, and are consequently an active area of research.

A landmark in the exploration of fundamental energy costs of computation was the 1961 observation by Rolf Landauer that the act of destroying a single bit of information requires at least $k \cdot T \cdot ln 2$ joules of energy, where $k$ is the Boltzmann constant ($1.38 \cdot 10^{-23}$ J/K), $T$ is the absolute temperature in degrees Kelvin, and $ln 2$ is the natural logarithm of $2$. The attachement of this lower limit to the destruction of information implies that the cost might be avoided by building systems that are lossless from an information standpoint: if information loss implies energy loss, a key to energy-efficient computations is to make them preserve information.

Landauer and others proposed that low-energy computations be performed using only information-preserving operations. They observed that for common functions like NAND or the exclusive-or (XOR) shown to the left -- comprising 2 bits of input information but producing a single output bit -- information is necessarily lost: the inputs cannot be reconstructed from the output values. Consequently on each XOR operation some information is lost, with the consequent accrued energy cost as dictated by the Landauer limit. If however we restrict our basic logical operations to information-preserving functions like the Feynman gate shown to the right, and carefully preserve all output information (even that not required for our computation), we might avoid this energy penalty. Note that the $Q$ output of the Feynman gate carries the same information as the output of the XOR gate, but the additional $P$ output disambiguates the input combination generating this output.

Landauer and his disciples observed that such lossless computation can be made reversible: since no information is lost in each step of the computation, it may be run backward as well as forward. Although construction of a completely reversible computer system presents some interesting challenges (e.g. input/output operations), it is conceptually feasible to perform arbitrarily complex computations reversibly. Imagine, for example, an intricate and time-consuming analysis that produces a valuable single-bit result. We start this computation on a reversible computer in some pristine initial state, perhaps with a large memory containing only zeros. As the computation progresses using reversible operations, extraneous outputs are saved in the memory, which gradually fills with uninteresting data. During this process, we may pump energy into the computer to effect its state changes, but theoretically none of this energy is dissipated as heat. When we have computed our answer, we write it out (irreversibly) at a tiny energy cost. We then run our computation in reverse, using the stored extraneous data to step backwards in our computation; in the process, we get back any energy we spent during the forward computation. When the backward phase is completed, the machine state has been returned to its pristine initial state (ready for another computation), we have our answer, and the only essential energy cost has been the tiny amount needed to output the answer.

Such thought experiments in reversible computation seem (and are) somewhat far-fetched, but provide important conceptual models for understanding the relation between laws of physics and those of information. Reversible computing plays an important role in contemporary research, for example in the area of quantum computing.

6.6. Further Reading

• Moore, G., "Cramming More Components onto Integrated Circuits", Electronics, v 36 no 8, April 19, 1965. 1965 paper observing that the optimal transistor count for a chip seemed to double ever two years, and predicting that growth rate to continue for "at least 10 years". This conservative prediction predates the popularity of CMOS (and many other subsequent technological breakthroughs), and has come to be known as Moore's Law.
• Landauer, Rolf, "Irreversibility and heat generation in the computing process", IBM J. Research and Development, 1961. 1961 paper exploring the theoretical limit of energy consumption of computation. Establishes a lower bound on the energy cost of erasing a bit of information, and hence of irreversible computation.

6.7. Chapter Summary

The CMOS technology described in this chapter has become the tool of choice for implementing large digital systems, and for a number of good reasons:

• Effective manufacturing techniques allow economical manufacture of reliable devices containing billions of logic elements;
• Quiescent CMOS circuits have virtually zero power dissipation;
• CMOS gates are naturally lenient combinational devices.

Key elements of the CMOS engineering discipline include:

• The use of complementary transistor types, NFETs and PFETs, within each CMOS gate;
• Each CMOS output is a circuit node connected to an NFET-based pulldown circuit as well as a PFET-based pullup circuit, where for every combination of inputs either the pullup connects the output to $V_{dd}$ or the pulldown connects the output to ground;
• Each single CMOS gate is naturally inverting: positive input transitions can cause only negative output transitions, and vice versa. Hence certain logic functions cannot be implemented as a single CMOS gate and require multiple-gate implementations;
• High gain in the active region allows large noise margins, hence good noise immunity.
• Transitions take time: pumping charge into or out of an output node is work (in the physical sense) and cannot happen instantaneously. This leads to finite rise and fall times, which we accommodate in our $t_{pd}$ specifications.

Although single CMOS gates are naturally lenient, we observe that acyclic circuits of CMOS gates are not necessarily lenient. If lenience is required of a CMOS circuit, it can be assured by an appropriate design discipline.